La caida de los cuerpos

Todos sabemos que la gravedad es de 9,8m/s2. ¿Pero qué es la gravedad? La gravedad es la aceleración que sufre un objeto cuando cae. Si tiramos una bola, y vamos tomando cuánto recorre cada cierto tiempo, podemos ver que este intervalo es mayor cada vez. Podemos también calcular cuál es la velocidad, y después, la aceleración (la gravedad).
Tras realizar este experimento, los datos obtenidos respecto a las posiciones son estos:

La gráfica obtenida es una parábola, y se puede ver claramente como el intervalo va aumentando. La velocidad es la superficie que recorre un móvil cada cierto tiempo, y nosotros, con estos datos, podemos calcular cual es la velocidad instantánea.
Así: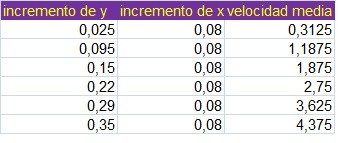  v (t) = incremento de y/incremento de t

La y representa la longitud y la x el tiempo. En teoría, el aumento de la velocidad ha de ser todo el rato el mismo, ya que la aceleración es constante.
Aquí podemos ver una gráfica de cómo aumenta la velocidad

En teoría, esta gráfica tendría que ser totalmente una recta, ya que la aceleración es constante. No lo es debido a errores a la hora de tomar los datos, que nunca van a ser exactos. Sin embargo, pese a estos errores, se puede ver que la gráfica es un MRUA, es decir, un movimiento rectilíneo uniformemente acelerado.

Ahora podemos calcular cual es la gravedad. Podemos hacerlo de dos formas.
Una de ellas se basa en que la aceleración es el incremento de la velocidad respecto al tiempo. Por este medio podemos obtener los siguientes datos:

. 

Según estos datos, la gravedad cambia. Quitando el primero, en el que, evidentemente, se ha cometido un error, los demás rondan el 9,8. 
Si en lugar de hacerlo por tramos lo hacemos de forma general, obtendremos que la gravedad es 9,11 m/s2, es decir, que nuestro error es de solo 0,6.

La otra se basa en que la aceleración corresponde a la pendiente de la gráfica de velocidad respecto a tiempo, es decir, la gráfica anterior. Con esto obtenemos exactamente los mismo valores que en la tabla anterior, solo que de otra manera distinta.
Como ya hemos dicho, se cometen muchos errores. ¿Cuales? Es muy difícil tomar el tiempo exacto  en cada momento. También hay que tener en cuenta factores tales como el rozamiento con el aire, o que podemos empujar un poco la bola.
Ahora vamos a comparar los valores que en teoría nos tendrían que haber salido y los que nos han salido de verdad.
Empecemos con los de velocidad. La ecuación para obtener la velocidad de una caída libre es v(t)=v·t
Nuestros datos son
Sin embargo, deberíamos haber obtenido los siguientes datos:

Otra vez, los datos cambian debido a los errores cometidos.
Ahora vamos con las posiciones. En esta ocasión la ecuación es g/2 · t2
Nuestros datos son
Y sin embargo, con la ecuación salen:
Así que, en conclusión, los objetos en caida libre sufren una aceleración que en teoría es 9,8m/s2, pero que a nosotros nos sale 9,11m/s2 debido a errores cometidos.

ACTIVIDAD 1: ARQUÍMEDES. EL PRINCIPIO FUNDAMENTAL DE LA HIDROSTÁTICA.

Para hacer esta entrada, nos hemos ayudado del primer capítulo del libro que estamos leyendo (De Arquímedes a Einstein), que es el que trata sobre Arquímedes.
Para poder realizar unos experimentos, debemos saber lo que son el dinamómetro, la báscula y el calibre.
El dinamómetro es un instrumento utilizado para medir fuerzas o para pesar objetos. Fue inventado por Isaac Newton.
Posee un muelle, que se encuentra en un cilindro que a su vez puede estar introducido en otro cilindro. Además tiene dos ganchos, uno en cada extremo. En el cilindro externo hay unas marcas con una escala, en unidades de fuerza.Cuando cuelgas pesos o ejercer fuerza en el gancho, el cursor que hay en el interior se mueve, indicando el valor de la fuerza.
Hay otros instrumentos de medida de fuerzas, especialmente de pesos, que reciben nombres diversos, pero que en realidad son dinamómetros, porque su funcionamiento se basa en el alargamiento o compresión de muelles. La balanza de cocina es un ejemplo.
El dinamómetro tiene una alta precisión, ya que, nos permite calcular hasta 0,1 N, y es muy exacto también.
Foto

Calibre:
El calibre es un instrumento de medida de longitud. Tiene una precisión bastante alta, ya que nos puede llegar a dar información sobre hasta las décimas de milímetro, y por lo tanto, mucho mayor que la de una regla o un metro normal. La exactitud es alta, siempre y cuando no nos equivoquemos al tomar la medida. Se utiliza, sobre todo, para medir los radios, y diámetros de las cosas. Aquí tenéis una página de wikipedia que te enseña de una manera bastante buena y fácil de entender como utilizar el aparato http://commons.wikimedia.org/wiki/File:Using_the_caliper_new.gif?uselang=es
Y aqui teneis una foto del aparato:

Báscula: 
La báscula es un aparato que sirve para pesar, o bien el peso, en las básculas con muelle elástico, o bien la masa, en básculas con contrapeso. Lo característico de las básculas es que tienen una plataforma a ras del suelo donde se sitúa el objeto o persona que se va a pesar. Es muy útil para pesar cuerpos mas grandes y pesados, ya que colocar el cuerpo encima de una plataforma es más sencillo que por ejemplo en una romana, que hay que colgarlo. Hay dos tipos: básculas mecánicas y electrónicas. Las electrónicas utilizan un sensor llamado celda de carga que tiene un precisión máxima de 1 en 10.000.
Un ejemplo de báscula:

Y luego determinada información sobre las magnitudes que miden, peso, masa y volumen.
El peso, en el sistema internacional, se mide en Newtons (N), aunque también se mide en ocasiones con el kilopondio (kp), que equivale a 9,80665N. La masa se mide, en el SI, con kilogramos, y el volumen con metros cúbicos, aunque tambien se utilizan los litros.
La unica magnitud fundamental de estas tres es la masa. El peso es una fuerza, y, por lo tanto, su ecuacion dimensional es M·L·T-2. La del volumen es L3.El peso, en el sistema internacional, se mide en Newtons (N), aunque también se mide en ocasiones con el kilopondio (kp), que equivale a 9,80665N. La masa se mide, en el SI, con kilogramos, y el volumen con metros cúbicos, aunque tambien se utilizan los litros.
La unica magnitud fundamental de estas tres es la masa. El peso es una fuerza, y, por lo tanto, su ecuacion dimensional es M·L·T-2. La del volumen es L3.

Empecemos con el experimento. Tenemos dos bolas, una negra y una plateada y vamos a compararlas en distintos aspectos.

Primero, vamos a comparar diferentes medidas experimentales con algunas teóricas.

Según la báscula, la masa de la bola plateada es de 68,5g y el de la negra 22,5g. Vamos a ver si utilizando la ecuación de P=m·g nos salen los mismo datos.

El peso, que sabemos gracias al dinamometro, de la bola plateada es de 0.68N. Por lo tanto:
P=m·g
0.67m/s2=m·9.8m/s2

m=0.0684kg=6.84·10-2kg
Y lo mismo con la bola negra:
P=m·g
0.22m/s2=m·9.8m/s2
m=0.0224kg=2.24·10 -2kg
Los resultados que salen en la ecuacion, al compararlos con los de la bascula, salen algo diferentes (6.84·10-2kg y 6.85·10-2kg; 2.24·10-2kg y 2.25·10-2kg, respectivamente) porque los datos tomados con el dinamómetro no son exactos y la báscula no son completamente exactos, ya que la medida nunca es exacta.

Algunas fotos del experimento:

Masa bola plateada

Masa bola negra

 

Peso bola plateada.

Peso bola negra.

Ahora, ya que sabemos el diámetro de las bolas gracias al calibre, calcularemos su volumen y luego la densidad.

radio= diametro/2= 2,51cm/2= 1,255cm
V=4/3 πr3= 4/3pi·1,2553=8,279cm3= 8,28cm3
Ahora la densidad de la bola plateada:
d=m/v
d=6,85·10-2 kg /8,28·10-6m3
d=8,27·10 -3 kg/cm3
Y la densidad de la bola negra:
d=m/v
d=2,25·10-2kg/ 8,28cm3
d=2,72·10 -3 kg/cm3

Diámetro bolas.

Ahora vamos con el empuje que haría el agua sobre nuestras bolas.
Bola plateada
Dinamometro sin agua = 0,67N
Dinamometro con agua= 0,59N
Empuje experimental:
E= Peso-Peso aparente= 0,67N- 0,59N= 0,8N
Empuje teorico:
E= Volumen de la esfera·Densidad del liquido · gravedad
E= 8,28cm3 ·1g/cm3 ·9,8m/s2= 8,28·10-6
Bola Negra
Dinamometro sin agua= 0,22N
Dinamometro con agua= 0,14N
Empuje experimental:
E=Peso-Peso Aparente= 0,22N-0,14N= 0,08N
Empuje teorico:
E= Volumen de la esfera·Densidad del liquido · gravedad
8,28cm3·1g/cm3·9,8m/s2= 8,28^·10-6
Aunque los resultados salen un poco diferente, porque, como ya hemos dicho, medir es equivocarse, se puede ver que ambos empujes son idénticos, de lo que se deduce que el ague ejerce la misma fuerza sea la que sea la masa del objeto. Claro esta que luego el empuje actuará de manera diferente en los objetos.

Introducción

Hola a todos, como pone en la descripción del blog, somos tres estudiantes de 4 de la ESO y hemos creado este blog para poder hablaros sobre varios aspectos de la Física.Esperamos que os divirtáis leyendo este blog, y que os parezca interesante.

Primero, os hablaremos un poco sobre el libro en general.

Para elegir los diez experimentos que figuran en el libro, el autor, Manuel Lozano Leyva, se basó en una lista creada por Robert Crease. Esta lista había sido hecha con el objetivo de que apareciese en la revista Physics World, pero tuvo más éxito de lo previsto y acabó apareciendo en muchos otros periódicos y revistas, como el New York Times o El País, este último en su número del 23 de octubre de 2002. Al leer la encuesta, según nos cuenta el propio autor en la introducción, decidió escribir un libro que hablara sobre los experimentos y su s autores, pero decidió cambiar uno de ellos, dado que había dos del mismo científico: Galileo. Así, sustituyendo uno por el undécimo clasificado de la lista, el principio de hidróstatica de Arquímedes, concluyó la lista en la que se basa el libro.

Aquí tenéis la noticia del País http://elpais.com/diario/2002/10/23/futuro/1035324001_850215.html
El hilo conductor del libro es la historia, dado que crean un eje cronológico perfecto, en el que solo desaparece la Edad Media.
En la asignatura, el libro nos puede motivar de diversas maneras. Por una parte, es una manera más didáctica de conocer experimentos importantes en la historia de la física, y por otra, nos puede ayudar a ver la clase de otra forma, mucho más “divertida”
Creo que es importante conocer la Historia de la Ciencia del mismo modo que es importante conocer la Historia en general: para poder entender cómo son las cosas hoy en día. Así, si sabemos que pensó alguien hace ya mucho tiempo, entenderemos mejor porque pensamos que las cosas funcionan en el modo en el que funcionan.
De los experimentos que figuran en el libro, todas las participantes del blog conocíamos el del principio fundamental de la hidróstatica, de Arquímedes, y el experimento de Galileo sobre la caída libre de los cuerpos.
Algunas conocíamos el de la descomposición de la luz, y otras la de la medida de la tierra. Sin embargo, ninguna conocíamos (al menos antes de leer el libro), los seis experimentos restantes, que, curiosamente, son los últimos seis capítulos, al ser los menos antiguos.
Respecto a los científicos, nos sonaban, como mínimo, los nombres de Arquímedes , Erastótenes, Galileo, Newton, Rutherford, Einstein y Bohr.

Hay otros muchos que no habíamos oído ni siquiera mencionar, como Cavendish, aunque iremos aprendiendo cosas sobre ellos a lo largo de la lectura del libro.

Análisis de la Ilustración

En la ilustración de la portada aparece un dibujo de Einstein, el conocido científico, en una bañera. Einstein aparece con el pelo revuelto y la lengua sacada, como en muchas fotografías suyas.



Además se encuentra en una bañera desbordándose, nos recuerda a la famosa anécdota de Arquímedes, que le hizo deducir su famoso principio, que nos permite saber el volumen de un cuerpo sólido e irregular.

Se ha querido relacionar de alguna forma estos dos grandes
científicos representándolos de maneras muy distintas en un mismo dibujo, Einstein con su retrato y Arquímedes con su experimento.

 

 

 

Hemos dedicido crear una portada alternativa, a ver que os parece:

 

Pese a la gran diferencia que existe entre las épocas de estos dos personajes (mientras que Arquímedes nació en 287 a.C, Einstein len 1879 d.C) en ambas la ciencia ha sido muy importante para el ser humano. Seguramente los descubrimientos de Arquímedes ayudaron a Einstein a realizar estudios, experimentos…que le llevaron a nuevos grandes descubrimientos muy significativos para la ciencia, que a su vez, ayudaron a la ciencia de hoy en día.

Biografía del autor

Manuel Lozano Leyva es el escritor de este libro sobre la historia de la física, De Arquímedes a Einstein. Es un físico nuclear y divulgador científico sevillano, y desde hace 18 años, catedrático de Física Atómica, Molecular y Nuclear en la facultad de Física de la Universidad de Sevilla. Además, ha representado durante seis años a España en el comité de expertos de física nuclear de la European Science Foundation.

Tras sus estudios doctorales en Oxford, trabajó en el Instituto Niels Bohr de Copenhague, la Ludwig Maximillian Universität de Munich, el Instituto Galileo Galilei de Padua y el CERN (Centro Europeo de Investigaciones Nucleares).
Es uno de los mejores divulgadores científicos de España, ya que tiene mucha fe en la ciencia y ha publicado "El cosmos en la palma de la mano" (2002); "De Arquímedes a Einstein" (2005); "Los hilos de Ariadna" (2007); "Nucleares ¿por qué no?" (2009).


También es colaborador de la prensa en la columna del suplemento de Ciencia,
del diario Público y de los periódicos del Grupo Joly. Y además ha participado
en el programa Redes de TVE2 (en Vida extraterrestre y en El tiempo no existe).